La proiezione conica conforme di Lambert è prodotta matematicamente dalla semplice proiezione conica. Un cono taglia la Terra in due cerchi, che sono chiamati Paralleli Standard. La latitudine a metà, tra i paralleli standard, è definita come la latitudine del parallelo di origine.
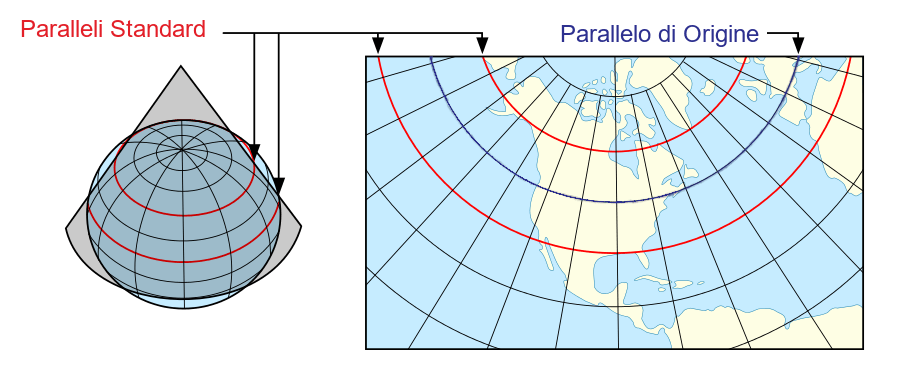
Come si può notare dalla figura, i paralleli si trasformano in archi di circonferenze concentriche, mentre i meridiani si trasformano in linee rette che si irradiano dal Polo di proiezione.
La carta di Lambert ha le seguenti proprietà:
- I Meridiani appaiono come linee rette che si irradiano dal Polo di proiezione.
- I Paralleli di latitudine sono archi di cerchi concentrici concavi alla proiezione del Polo con spaziatura quasi costante.
- Le linee lossodromiche sono curve concave al Polo di proiezione, ad eccezione dei meridiani che appaiono come linee rette.
- Le ortodromie sono curve concave al Parallelo di origine, ad eccezione dei meridiani che appaiono come linee rette. Tuttavia, un Cerchio massimo rappresenta quasi una linea retta quando collega due posizioni che si trovano al Parallelo di origine. Ai fini della pianificazione, si può presumere che i cerchi massimi siano linee rette.
- La Convergenza del grafico è costante e non cambia con la latitudine. Ciò si verifica perché i meridiani sono linee rette.
La formula per la convergenza del grafico è: Convergenza del grafico = differenza di longitudine x il seno del (parallelo di origine). Da questa formula possiamo concludere che la Convergenza del grafico e la Convergenza della Terra (Convergenza terrestre = differenza di longitudine x seno della Latitudine media ) sono uguali solo quando le due posizioni si trovano sul Parallelo di origine.
La scala della carta conforme di Lambert:
- È corretta sui paralleli standard.
- Si espande (aumenta) al di fuori dei paralleli standard.
- Si contrae (diminuisce) in mezzo ai paralleli standard e raggiunge il suo valore minimo al Parallelo di origine.